How Do You Know When a Statistics Problem Is Two Sided

When you bear a exam of statistical significance, whether information technology is from a correlation, an ANOVA, a regression or some other kind of test, you lot are given a p-value somewhere in the output.  If your examination statistic is symmetrically distributed, yous tin can select ane of three alternative hypotheses. Two of these correspond to 1-tailed tests and i corresponds to a two-tailed test.  However, the p-value presented is (almost always) for a 2-tailed test.  But how practise you choose which test?  Is the p-value appropriate for your test? And, if it is not, how can you summate the right p-value for your test given the p-value in your output?

What is a two-tailed test?

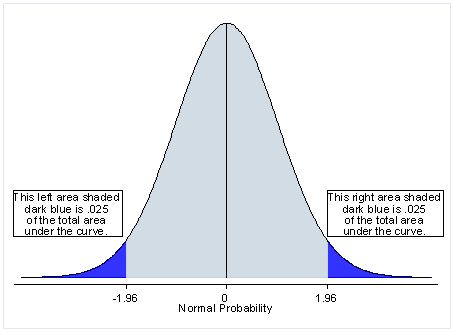
First let's offset with the significant of a two-tailed examination.  If y'all are using a significance level of 0.05, a ii-tailed test allots half of your alpha to testing the statistical significance in one direction and half of your blastoff to testing statistical significance in the other direction.  This ways that .025 is in each tail of the distribution of your test statistic. When using a ii-tailed examination, regardless of the direction of the relationship you hypothesize, you are testing for the possibility of the relationship in both directions.  For case, we may wish to compare the mean of a sample to a given value 10 using a t-test.  Our null hypothesis is that the mean is equal to x. A two-tailed test volition test both if the mean is significantly greater than x and if the mean significantly less than 10. The mean is considered significantly different from x if the examination statistic is in the height ii.5% or bottom 2.v% of its probability distribution, resulting in a p-value less than 0.05.

What is a one-tailed test?

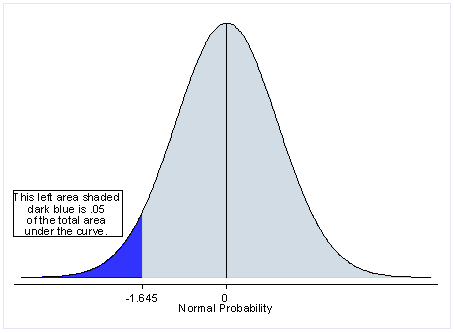
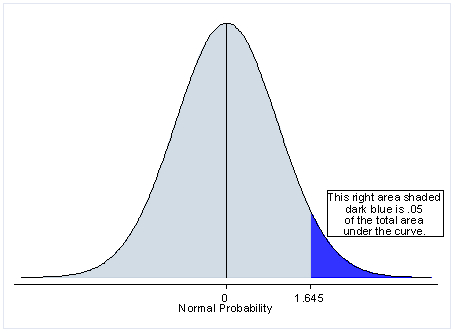
Next, let's discuss the meaning of a ane-tailed test.  If yous are using a significance level of .05, a one-tailed test allots all of your alpha to testing the statistical significance in the one direction of interest.  This means that .05 is in ane tail of the distribution of your examination statistic. When using a i-tailed examination, you are testing for the possibility of the relationship in one direction and completely disregarding the possibility of a relationship in the other direction.  Let's return to our example comparing the mean of a sample to a given value x using a t-test.  Our null hypothesis is that the hateful is equal to ten. A i-tailed test will examination either if the mean is significantly greater than ten or if the hateful is significantly less than ten, just not both. Then, depending on the chosen tail, the hateful is significantly greater than or less than x if the exam statistic is in the top 5% of its probability distribution or bottom 5% of its probability distribution, resulting in a p-value less than 0.05.  The one-tailed examination provides more power to notice an effect in ane direction by not testing the effect in the other direction. A give-and-take of when this is an appropriate option follows.

When is a 1-tailed test appropriate?

Because the one-tailed examination provides more ability to detect an issue, you may be tempted to apply a 1-tailed test whenever you have a hypothesis about the management of an effect. Before doing so, consider the consequences of missing an effect in the other direction.  Imagine you accept developed a new drug that you believe is an improvement over an existing drug.  You wish to maximize your ability to notice the improvement, then yous opt for a 1-tailed test. In doing so, you fail to test for the possibility that the new drug is less effective than the existing drug.  The consequences in this example are farthermost, just they illustrate a danger of inappropriate employ of a one-tailed exam.

So when is a one-tailed exam appropriate? If yous consider the consequences of missing an consequence in the untested direction and conclude that they are negligible and in no way irresponsible or unethical, then you can proceed with a one-tailed exam. For case, imagine once again that you take adult a new drug. It is cheaper than the existing drug and, you believe, no less effective.  In testing this drug, you are but interested in testing if it less effective than the existing drug.  You do non care if it is significantly more constructive.  Y'all just wish to testify that it is not less effective. In this scenario, a i-tailed exam would be appropriate.

When is a ane-tailed test Not appropriate?

Choosing a one-tailed exam for the sole purpose of attaining significance is not appropriate.  Choosing a one-tailed test after running a two-tailed test that failed to reject the null hypothesis is non appropriate, no matter how "close" to significant the two-tailed exam was.  Using statistical tests inappropriately tin lead to invalid results that are not replicable and highly questionable–a steep price to pay for a significance star in your results tabular array!

Deriving a one-tailed test from two-tailed output

The default amid statistical packages performing tests is to written report two-tailed p-values.  Because the most commonly used test statistic distributions (standard normal, Student's t) are symmetric virtually zero, nigh one-tailed p-values can be derived from the two-tailed p-values.

Beneath, nosotros have the output from a two-sample t-test in Stata.  The test is comparison the mean male person score to the hateful female score.  The naught hypothesis is that the divergence in means is zero.  The 2-sided culling is that the difference in ways is not goose egg.  There are two ane-sided alternatives that i could opt to exam instead: that the male score is higher than the female score (diff  > 0) or that the female score is college than the male score (unequal < 0).  In this instance, Stata presents results for all three alternatives.  Under the headings Ha: diff < 0 and Ha: diff > 0 are the results for the one-tailed tests. In the eye, under the heading Ha: diff != 0 (which ways that the difference is non equal to 0), are the results for the two-tailed test.

Two-sample t examination with equal variances  ------------------------------------------------------------------------------    Group |     Obs        Mean    Std. Err.   Std. Dev.   [95% Conf. Interval] ---------+--------------------------------------------------------------------     male |      91    50.12088    1.080274    10.30516    47.97473    52.26703   female person |     109    54.99083    .7790686    8.133715    53.44658    56.53507 ---------+-------------------------------------------------------------------- combined |     200      52.775    .6702372    ix.478586    51.45332    54.09668 ---------+--------------------------------------------------------------------     diff |           -4.869947    one.304191               -7.441835   -2.298059 ------------------------------------------------------------------------------ Degrees of freedom: 198                   Ho: mean(male) - mean(female person) = diff = 0      Ha: unequal < 0               Ha: diff != 0              Ha: diff > 0        t =  -3.7341                t =  -three.7341              t =  -3.7341                P < t =   0.0001          P > |t| =   0.0002          P > t =   0.9999              

Note that the exam statistic, -3.7341, is the same for all of these tests.  The two-tailed p-value is P > |t|. This tin can be rewritten equally P(>three.7341) + P(< -iii.7341).  Considering the t-distribution is symmetric nearly zero, these two probabilities are equal: P > |t| = 2 *  P(< -3.7341).  Thus, we can see that the 2-tailed p-value is twice the one-tailed p-value for the culling hypothesis that (diff < 0).  The other one-tailed culling hypothesis has a p-value of P(>-3.7341) = 1-(P<-3.7341) = ane-0.0001 = 0.9999.   And then, depending on the management of the ane-tailed hypothesis, its p-value is either 0.five*(ii-tailed p-value) or one-0.5*(ii-tailed p-value) if the examination statistic symmetrically distributed well-nigh zero.

In this example, the two-tailed p-value suggests rejecting the nada hypothesis of no deviation. Had nosotros opted for the one-tailed exam of (diff > 0), we would fail to reject the nada because of our choice of tails.

The output below is from a regression analysis in Stata.  Unlike the example above, merely the two-sided p-values are presented in this output.

                Source |       SS       df       MS              Number of obs =     200 -------------+------------------------------           F(  2,   197) =   46.58        Model |  7363.62077     2  3681.81039           Prob > F      =  0.0000     Residue |  15572.5742   197  79.0486001           R-squared     =  0.3210 -------------+------------------------------           Adj R-squared =  0.3142        Total |   22936.195   199  115.257261           Root MSE      =  8.8909 ------------------------------------------------------------------------------        socst |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval] -------------+----------------------------------------------------------------                                  science |   .2191144   .0820323     2.67   0.008     .0573403    .3808885                                math |   .4778911   .0866945     5.51   0.000     .3069228    .6488594        _cons |   fifteen.88534   3.850786     4.13   0.000     8.291287    23.47939 ------------------------------------------------------------------------------

For each regression coefficient, the tested null hypothesis is that the coefficient is equal to zero.  Thus, the one-tailed alternatives are that the coefficient is greater than cypher and that the coefficient is less than zero. To get the p-value for the ane-tailed test of the variable scientific discipline having a coefficient greater than nothing, you would split the .008 by ii, yielding .004 because the effect is going in the predicted direction. This is P(>2.67). If you had made your prediction in the other direction (the reverse direction of the model effect), the p-value would accept been 1 – .004 = .996.  This is P(<2.67). For all three p-values, the test statistic is two.67.

luttrellthappere55.blogspot.com

Source: https://stats.oarc.ucla.edu/other/mult-pkg/faq/general/faq-what-are-the-differences-between-one-tailed-and-two-tailed-tests/

Share this post